Numerical continuation is a predictor-corrector method that follows paths of equilibria or periodic solutions in one or more parameters. It is a popular approach for conducting a bifurcation analysis on a mathematical model of a nonlinear dynamic system. One of the benefits of numerical continuation over direct numerical simulations at different parameter values is that the stability and the basins of attraction of the solutions are unimportant to the method, which allows one to track entire solutions families and systematically detect bifurcations. Identified bifurcations can in turn be tracked as parameters are varied.
In this context, my research targets the extension of numerical continuation techniques to real-life engineering applications. To this end, I work on 1) improving the current capabilities of numerical continuation techniques, and 2) developing nonlinear model reduction techniques that can reduce the dimensionality of the mathematical models in hand while capturing the essential nonlinear dynamic behaviour of the system.
Bifurcation Analysis
Bifurcations are arguably one of the most important manifestations of nonlinearity. They represent stability boundaries in parameter space where dramatic qualitative and quantitative changes in the dynamics of a system can occur.

In this paper, the popular harmonic balance technique is combined with numerical continuation and bifurcation analysis tools in order to detect and track in parameter space the bifurcations of nonlinear mechanical structures. The proposed method was validated on the SmallSat satellite structure, a complex, real-life example that contains a relatively large number of degrees of freedom and piecewise-smooth nonlinearities.
Nonlinear Model Reduction
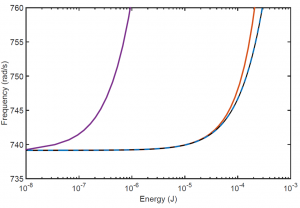
When the structure is linear with spatially-localized nonlinearities, classical linear reduction methods, such as the Craig-Bampton technique, can be used to accurately and effectively reduce the dimensionality of the linear system. However, when the system possesses nonlinearities distributed among all the degrees of freedom, as, for instance, when nonlinear geometric effects caused by large displacements and rotations are present, such linear reduction approaches proved ineffective.
In this paper, the nonlinear finite element models of three structures possessing geometric nonlinearities are reduced using a nonlinear coordinate transformation (quadratic manifold) and the concept of modal derivatives. The paper shows that modal derivatives can capture the distortions introduced by nonlinearity. The reduced-order model can in turn be used to accurately compute the nonlinear normal modes of the considered structures.