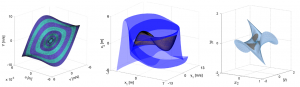
Nonlinear normal modes (NNMs) represent the analogue of linear normal modes (LNMs) for nonlinear systems. Although NNMs do no have some of the key mathematical properties of LNMs (such as orthogonality), NNMs share a number of important similarities with LNMs and proved useful to explain a number of nonlinear phenomena (modal interactions, localisation, energy transfers, etc.) One key similarity between NNMs and LNMs is the possibility to test a physical (damped) system and directly measure the NNMs of the underlying conservative system. Another similarity, directly related to the previous one, is the defining role that NNMs have on the frequency response of the nonlinear, damped system. In fact, NNMs usually describe well the dependence of the resonance frequencies of a system in function of the amplitude of oscillation, tracing out the so-called backbone curves.
In the context of nonlinear modal analysis, I specifically work on:
- the development of rigorous and effective computational methods for NNMs;
- the understanding of the role played by NNMs in the (global) dynamics of nonlinear systems;
- the development of experimental and mathematical analysis tools that can measure/identify the NNMs of a physical system.
Computation of NNMs
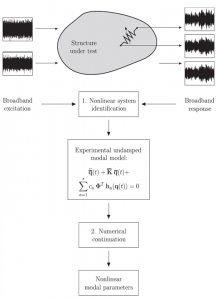
This paper reviews the recent advances in computational methods for nonlinear normal modes (NNMs). Different algorithms for the computation of NNMs for undamped and damped systems are presented, and their respective advantages and limitations are discussed. The methods are illustrated using various applications ranging from low-dimensional weakly nonlinear systems to strongly nonlinear industrial structures.
References: L. Renson et al. Numerical computation of nonlinear normal modes in mechanical engineering. JSV 364(2016)177–206. / L. Renson, Nonlinear Modal Analysis of Conservative and Nonconservative Aerospace Structures, PhD Thesis, University of Liège, 2014.
Evidence of Modal Interactions in a Spacecraft Structure
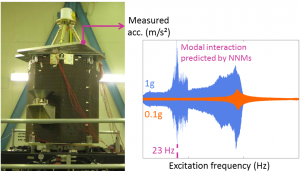
When excited at a constant frequency ω, nonlinear systems usually respond at that frequency and its harmonics (2ω, 3ω, …) – in fact, the response might also be non periodic as, for instance, in the case of quasi-periodic/chaotic oscillations. When one of these harmonics is close to the oscillation frequency of another NNM, a strong interaction between the two NNMs can occur, leading to (irreversible) energy transfers between the modes. As the oscillation frequency of a nonlinear system depends on the oscillation amplitude, such interactions can be realised without any integer ratio between the (linear) natural frequencies of the system.
Interactions between modes are not just mathematical curiosities and were observed on a number of physical systems, including real-life industrial structures such as the SmallSat satellite presented in Figure 1. In the papers below, the modal interactions observed experimentally were captured numerically by the NNMs of the system.
References: L. Renson et al. Complex dynamics of a nonlinear aerospace structure: numerical continuation and normal modes. Nonlinear Dyn (2015) 79:1293–1309. / J.P. Noel et al. Complex dynamics of a nonlinear aerospace structure: Experimental identification and modal interactions. JSV 333 (2014) 2588–2607.
Isolated Periodic Solutions and Energy Balance
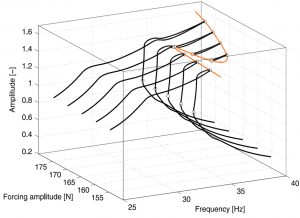
Families of isolated periodic solutions are frequently observed in the frequency response of nonlinear systems. Detached from the main resonance peaks, such solutions can hardly be observed using conventional simulations such as sine sweeps. Similarly, they are very difficult to observe experimentally. The presence of these isolas can lead to a significant underestimation of the response amplitude of the system at a particular excitation level.
This paper uses NNMs and an energy-balance technique to unveil the presence isolas. The proposed method allows to estimate the parameter values at which isolated solutions are present; estimates that can in turn be exploited by algorithms such as numerical continuation to capture the family of isolated solution.
References: R. J. Kuether, L. Renson, T. Detroux, C. Grappasonni, G. Kerschen, M.S. Allen. Nonlinear normal modes,modal interactions and isolated resonance curves. JSV 351(2015)299–310. / R. J. Kuether et al. Prediction of isolated resonance curves using nonlinear normal modes. Proceedings of the ASME IDETC/CIE 2015, Boston, USA.
Nonlinear Normal Modes for Nonconservative Systems – Invariant Manifolds
The most popular definition of NNMs is arguably the one that defines NNMs as periodic solutions of the conservative equations of motion. A concurrent work, which allows to extend NNMs to nonconservative (damped) systems, defines NNMs as two-dimensional invariant manifolds in phase space.
The first paper presents a finite-element-based method that can compute NNMs defined as 2D invariant manifolds for a wide range of (un)damped systems. The method relies on an explicit parameterization of the manifold and grows the surface as a collection of annular regions. However, the invariant manifold can a priori have a very complicated geometry including foldings; in which case an explicit parameterization fails. The second paper overcomes this issue by computing a NNM as a collection of trajectories in phase space. The third paper uses the theory of Koopman operators to provide a ‘global’ parameterization of the surface and its approximate expression in terms of a polynomial expansion.
References: L. Renson et al. An effective finite-element-based method for the computation of nonlinear normal modes of nonconservative systems. Meccanica (2014) 49:1901–1916. / L. Renson. C. Touze, G. Kerschen. Computation of damped nonlinear normal modes with internal resonances: a boundary value approach. Proceedings of the 8th ENOC, Wien 2014. /G.I. Cirillo, A. Mauroy, L. Renson, G. Kerschen, R. Sepulchre. A spectral characterization of nonlinear normal modes. 377 (2016) 284–301.
Identification of Nonlinear Normal Modes using a Nonlinear Phase Separation Technique
In linear modal analysis, the term phase separation usually refers to a range of mathematical techniques used to post-process experimental data and identify simultaneously multiple modes, separating their individual contributions from the data.
The first paper below extends this concept to nonlinear systems and proposes a nonlinear phase separation method that can extract multiple NNMs from broadband data collected during a single experiment. The method is demonstrated on numerical data collected on a structure composed of a clamped-clamped linear beam including a nonlinear spring. Time data were artificially corrupted with noise. The first experimental demonstration of the method was presented at the IMAC XXXV (second paper).
References: J. P. Noël, L. Renson, C. Grappasonni, G. Kerschen. Experimental modal analysis of nonlinear structures using broadband data. MSSP 74 (2016) 95–110. / L. Renson et al. Nonlinear Phase Separation Testing of an Experimental Wing-Engine Structure. Proceedings of the IMAC XXXV, Orange County, 2017.